Learning Eye-in-Hand Calibration from a Single Image

Learning Eye-in-Hand Camera Calibration from a Single Image

Eugene Valassakis*, Kamil Dreczkowski*, and Edward Johns

* Joint First Author Contribution

Published at CoRL 2021

Abstract

Eye-in-hand camera calibration is a fundamental and long-studied problem in robotics. We present a study on using learning-based methods for solving this problem online from a single RGB image, whilst training our models with entirely synthetic data. We study three main approaches: one direct regression model that directly predicts the extrinsic matrix from an image, one sparse correspondence model that regresses 2D keypoints and then uses PnP, and one dense correspondence model that uses regressed depth and segmentation maps to enable ICP pose estimation. In our experiments, we benchmark these methods against each other and against well-established classical methods, to find the surprising result that direct regression outperforms other approaches, and we perform noise-sensitivity analysis to gain further insights into these results.

Video

5-Minute Summary

Problem Setting

In this work, we study the problem of eye-in-hand camera calibration from a single image using deep learning methods. We constrain ourselves to not using any external apparatus, as long as part of the robot's end-effector is visible from the camera image to serve as the calibration object. Our models are trained entirely in simulation for deployment in the real world.

Three Different Models

We consider three natural alternatives for using deep learning in order to obtain the eye-in-hand camera calibration. One of those consists of an end-to-end method that maps images to poses, and two are geometric approaches that use deep learning to generate required inputs.

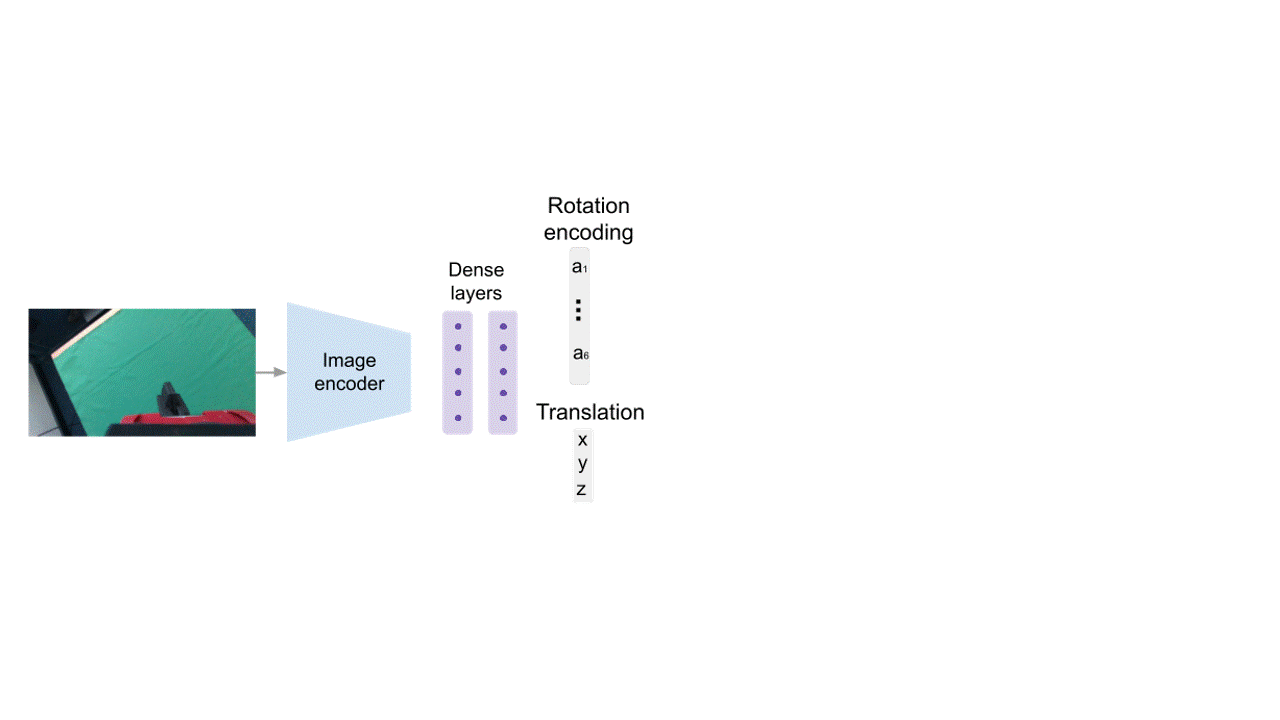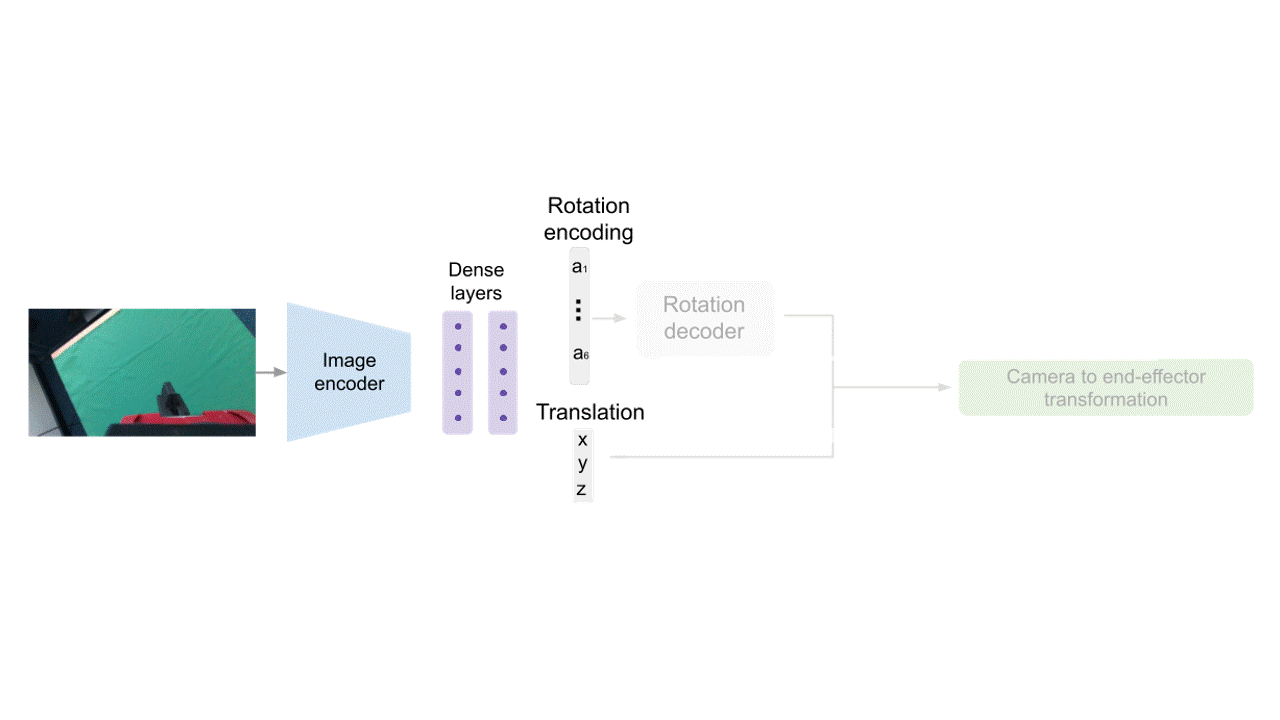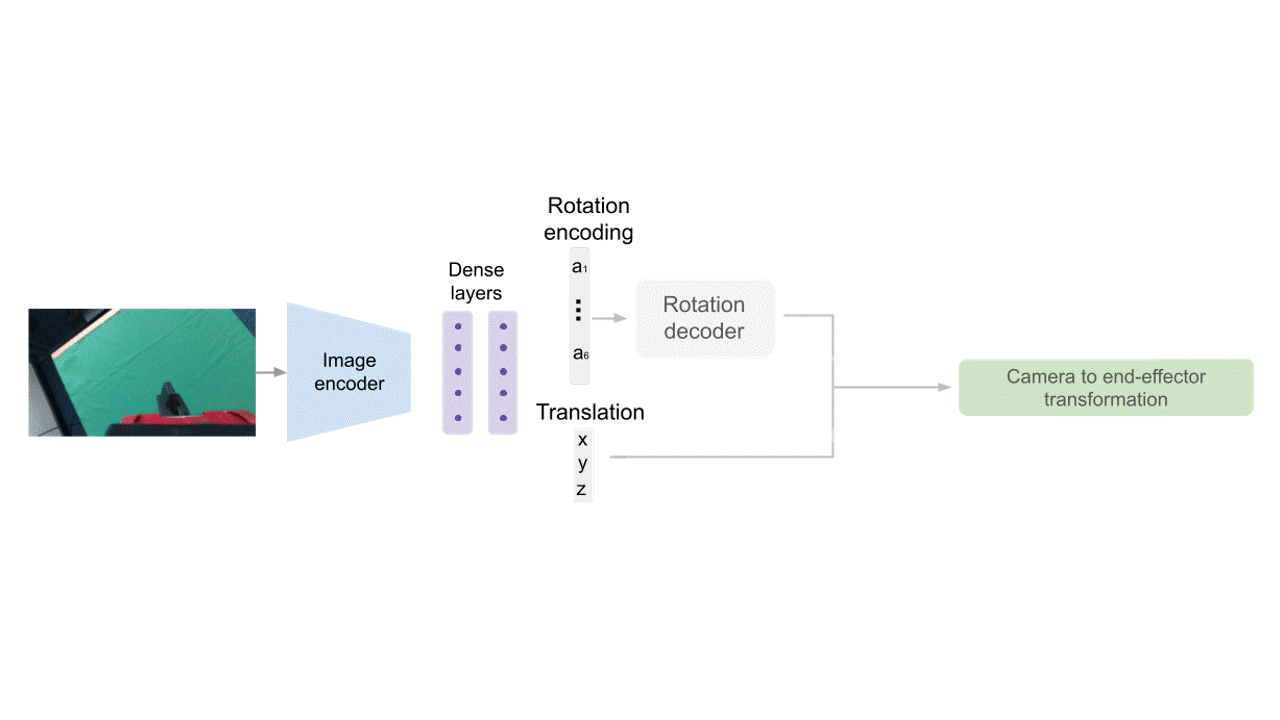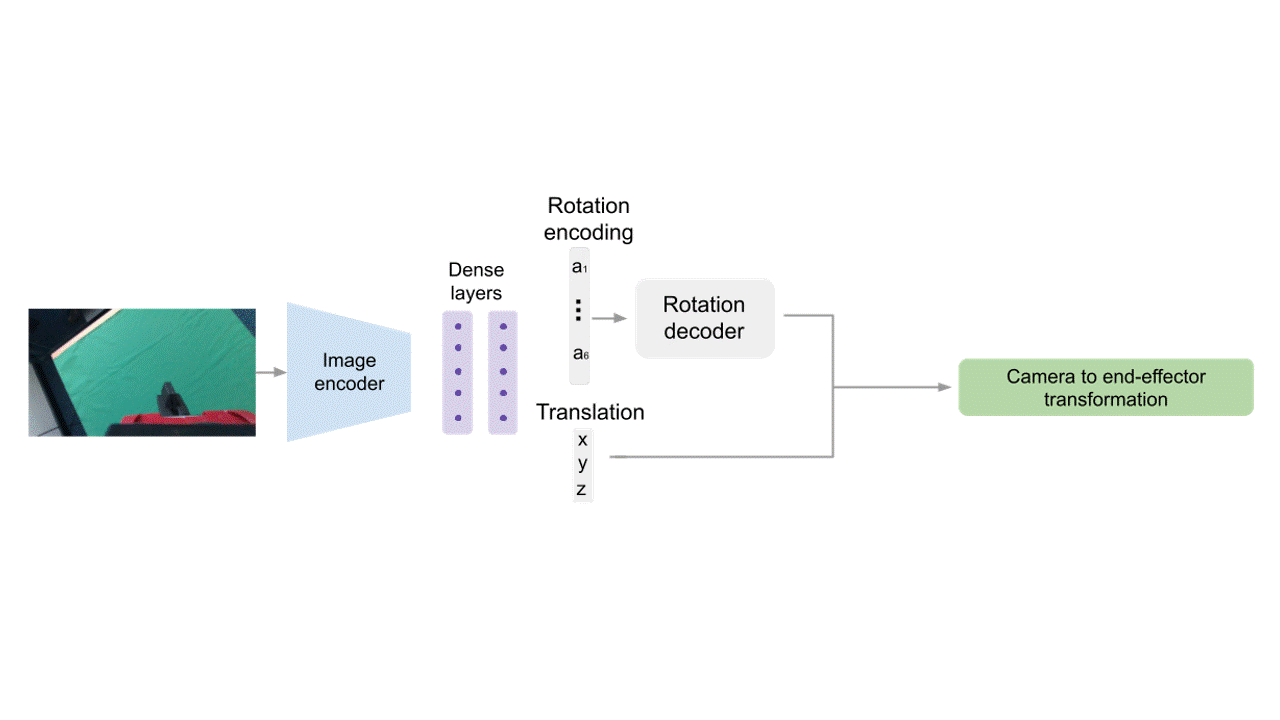
Direct Regression (DR)

For our end-to-end model, we use a direct regression approach. Given an input image, we use a series of convolutional and dense layers to predict an encoding of the rotation and translation of the camera with respect to the end-effector. After decoding those outputs, we obtain the camera-to-end-effector transformation.

Sparse Correspondence Model (SC)

Our sparse correspondence model is the first geometry-based, deep-learning enabled method we consider. It uses Perspective-n-Point (PnP) at its heart in order to compute the extrinsic matrix.

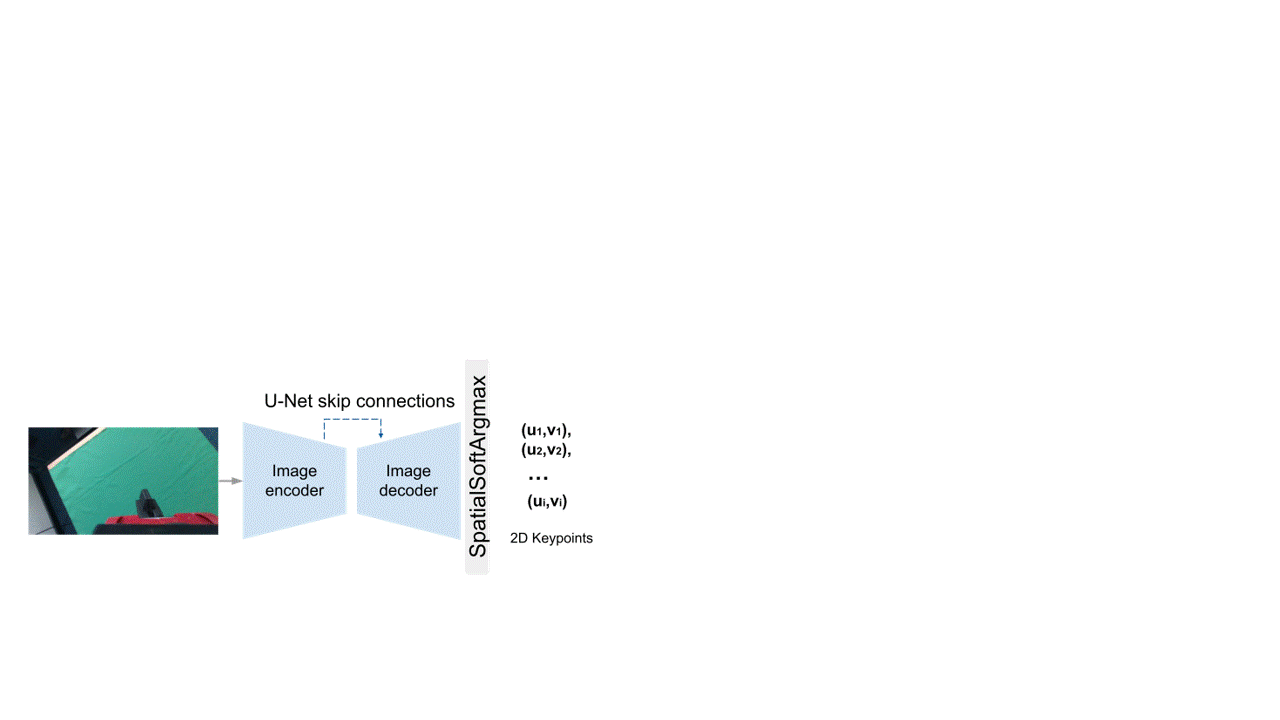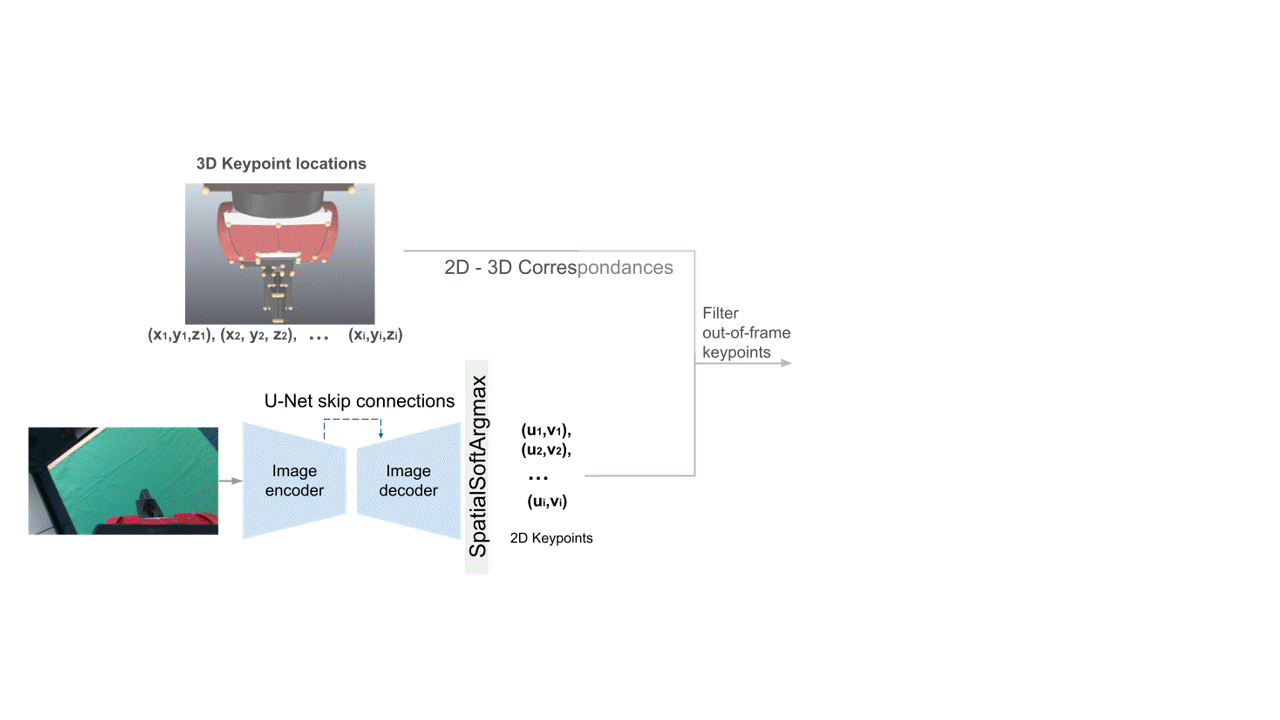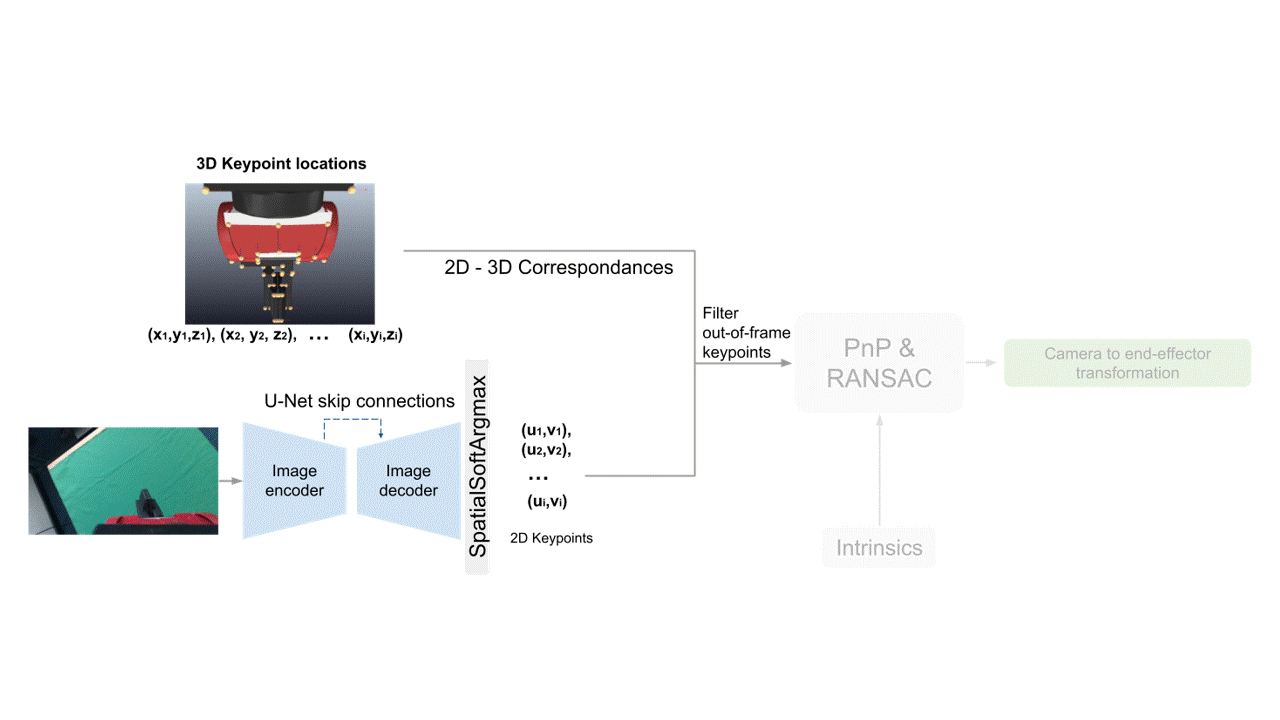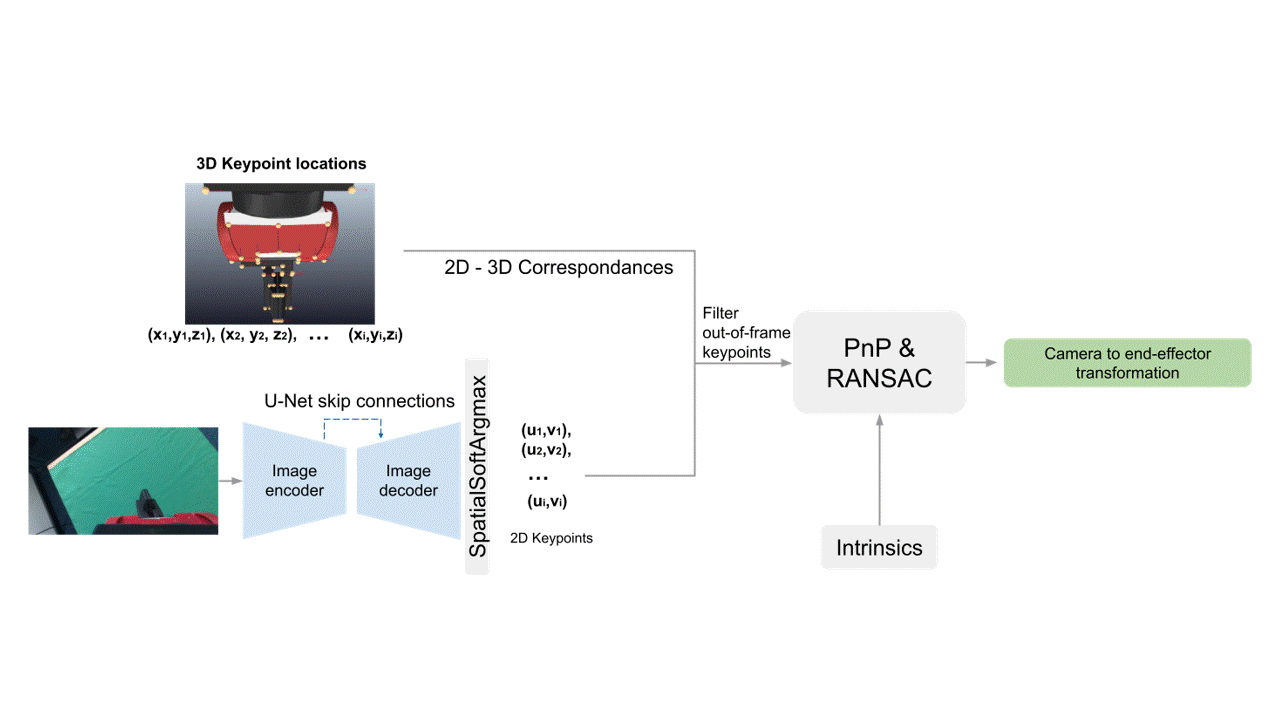
Starting from an input image, we use an encoder-decoder architecture to calculate the 2D image locations of a set of pre-defined 3D landmarks on the end-effector.

Using those, we then establish 2D-3D correspondences, and along with the intrinsics matrix, we use them as inputs to PnP, which outputs the camera-to-end-effector pose.

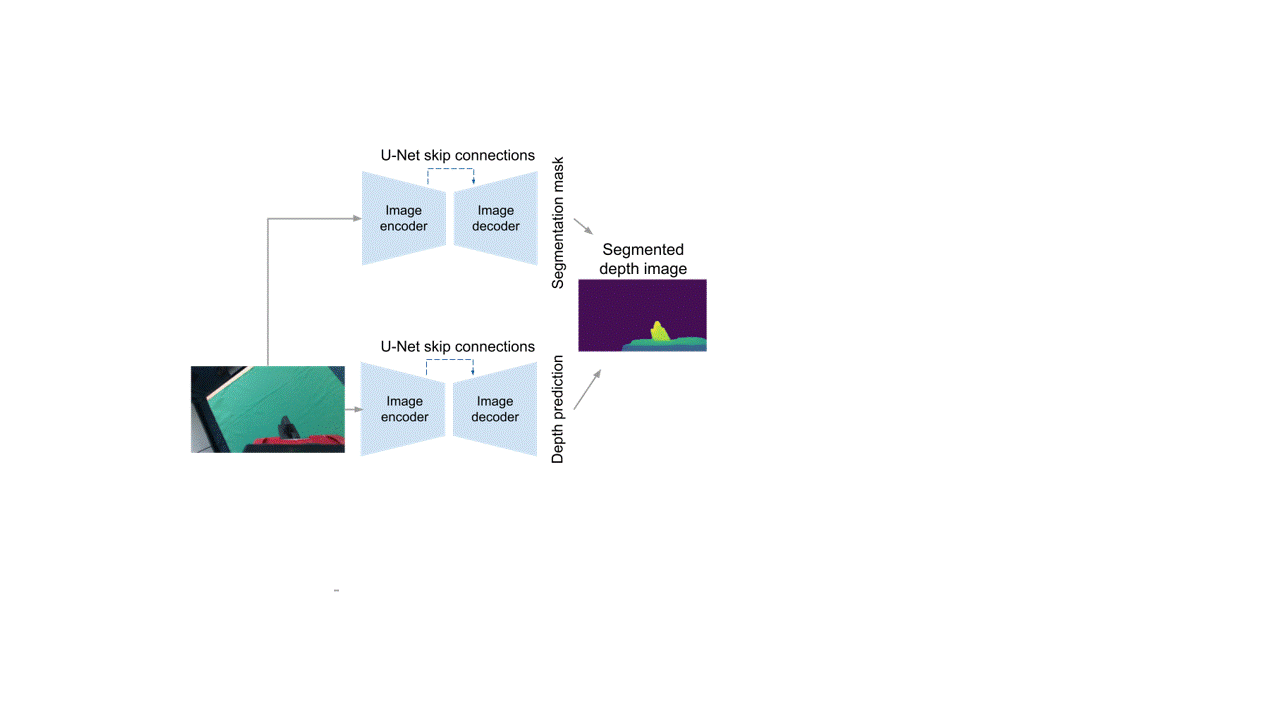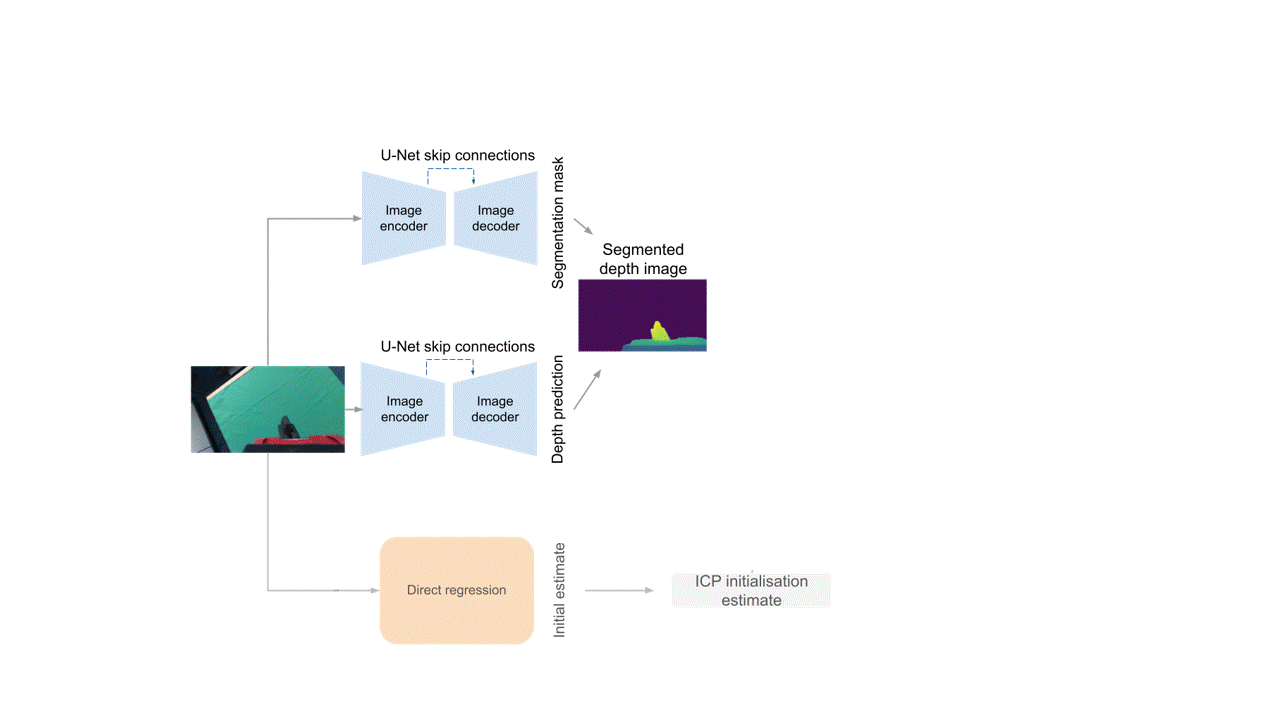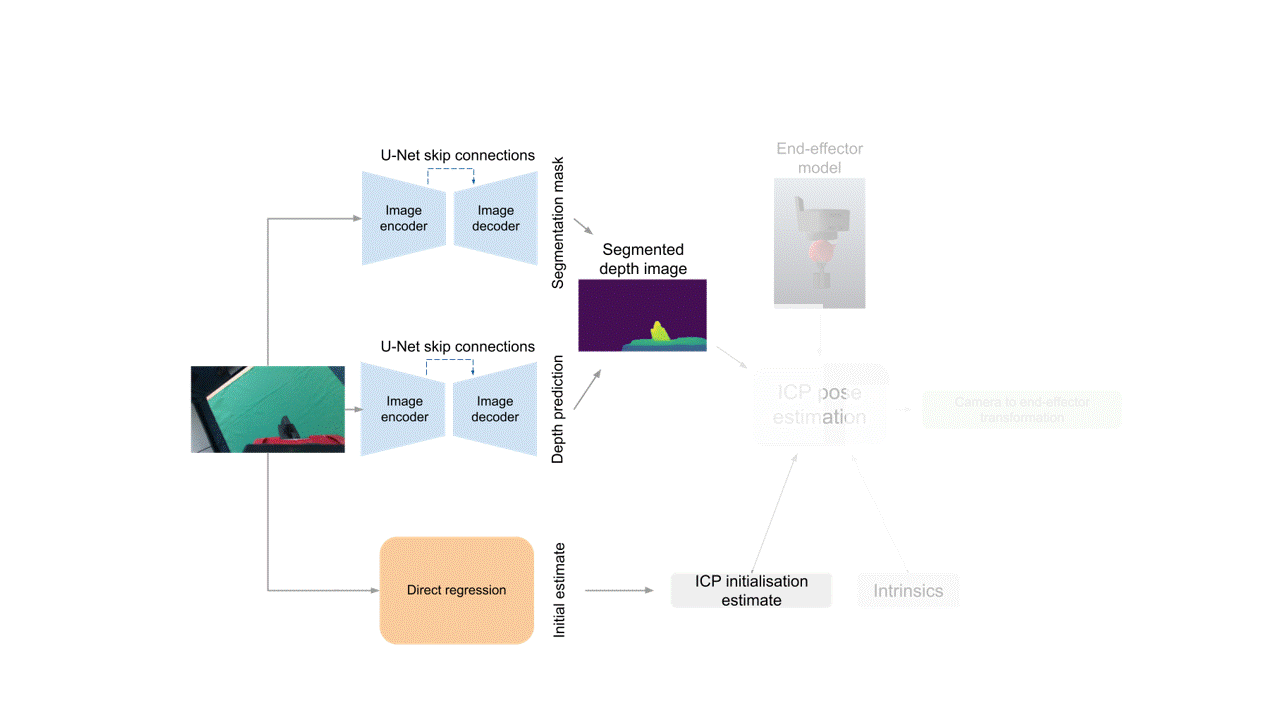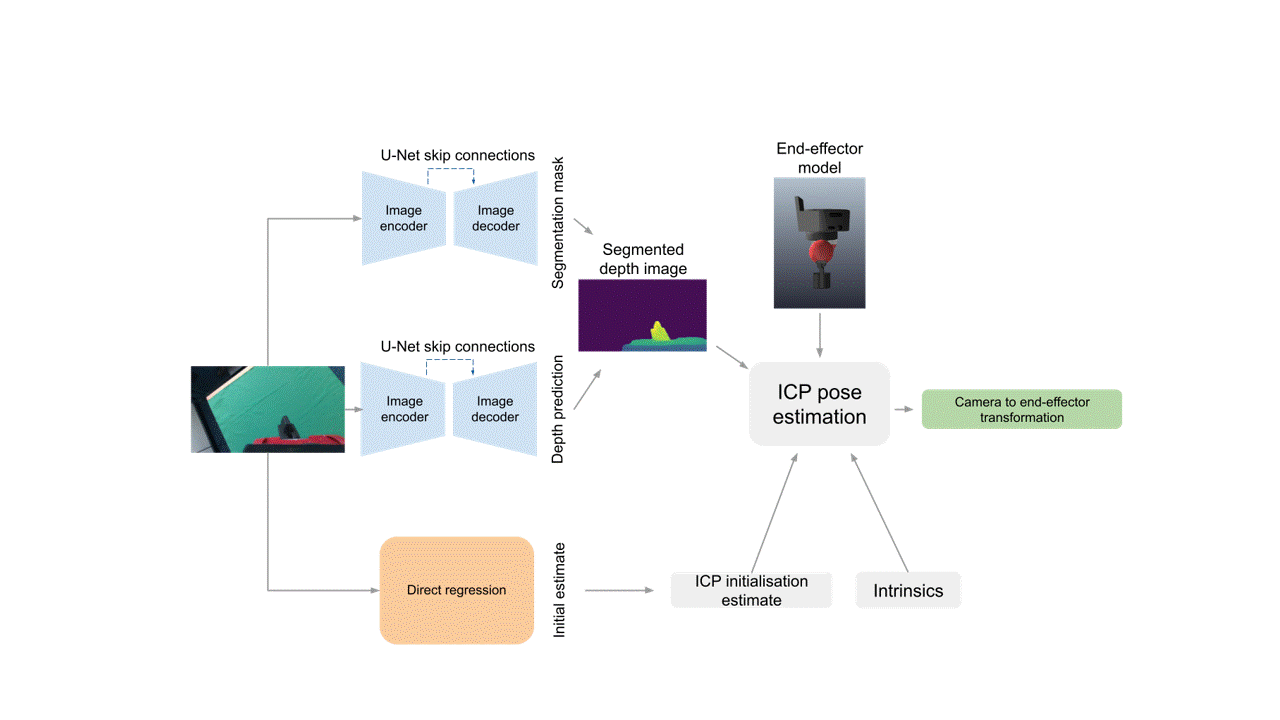
Dense Correspondence Model (DC)

Our dense correspondence model is built around the idea of using 3D point cloud registration in order to obtain the eye-in-hand calibration.

Starting from an input image, we first obtain a segmented depth image of the gripper by combining the outputs of a segmentation network and a depth prediction network.

Then, we use the direct regression model to obtain an initial estimate of the extrinsic matrix.

Finally, we use those as well as a model of the end-effector and the camera's intrinsic matrix as inputs to the Iterative Closest Point (ICP) algorithm, which computes the final camera-to-end-effector transformation.

Data Generation

We generate all our data in simulation, using domain randomisation to overcome the reality gap: We randomise the colours, lights, and textures of our simulator and add random background images.

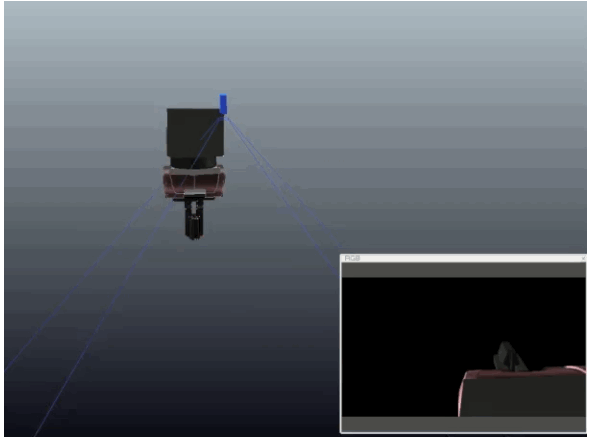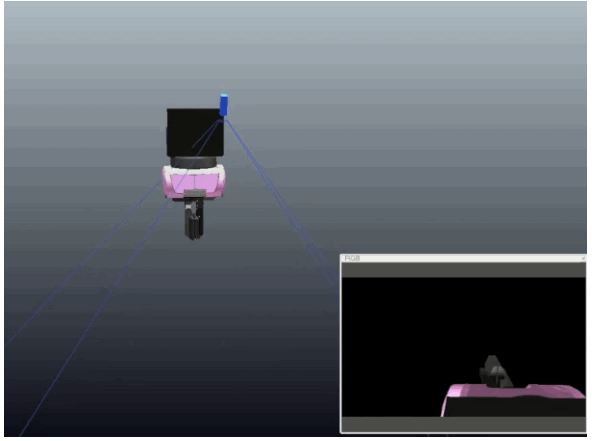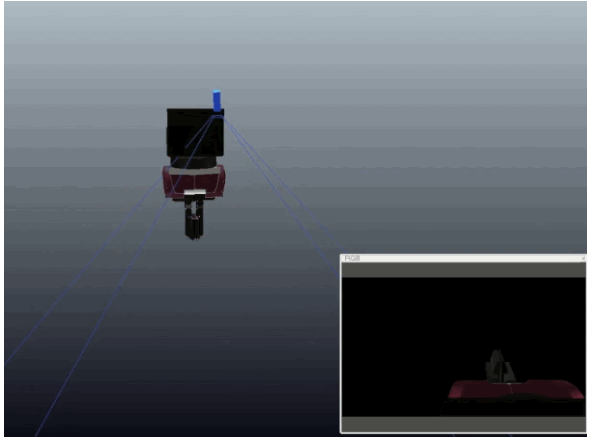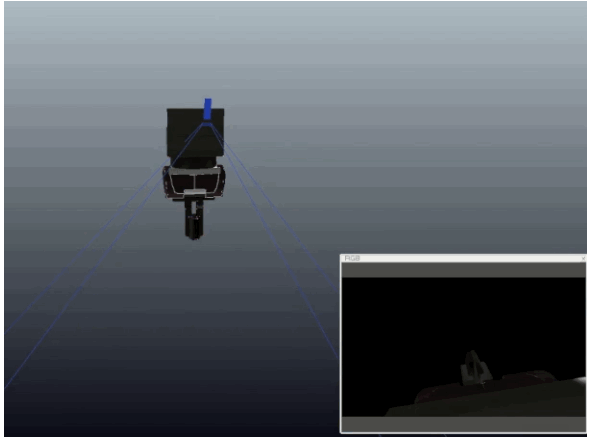
Experiments

We compare our method against well established classical baselines that require a calibration object and real-world data gathering for each new calibration. We perform simulation experiments where we evaluate the calibrations against ground truth values and real-world experiments where we use the spread of April tag position predictions from different viewpoints as a proxy for the error in the extrinsic calibration.

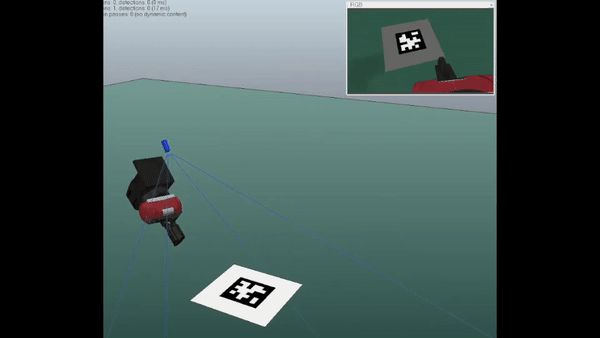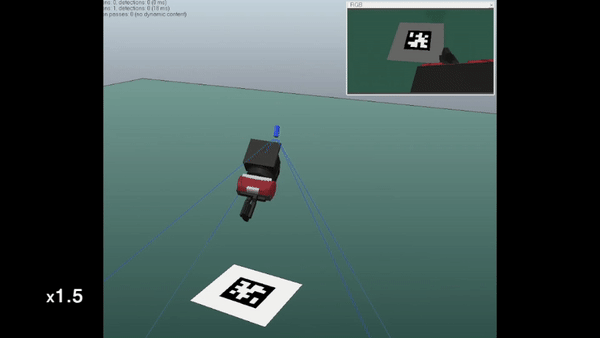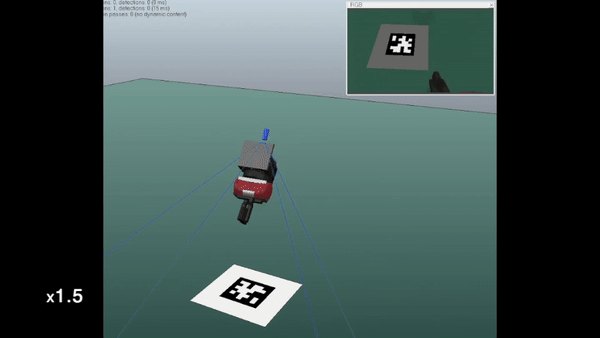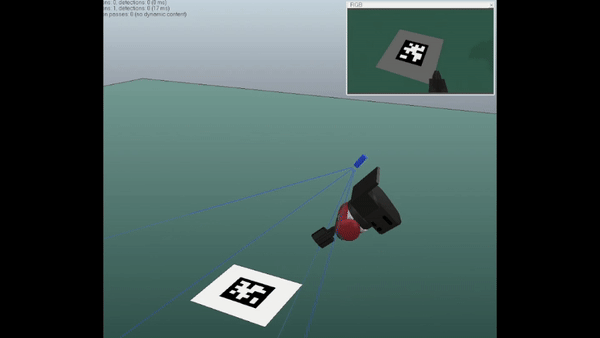
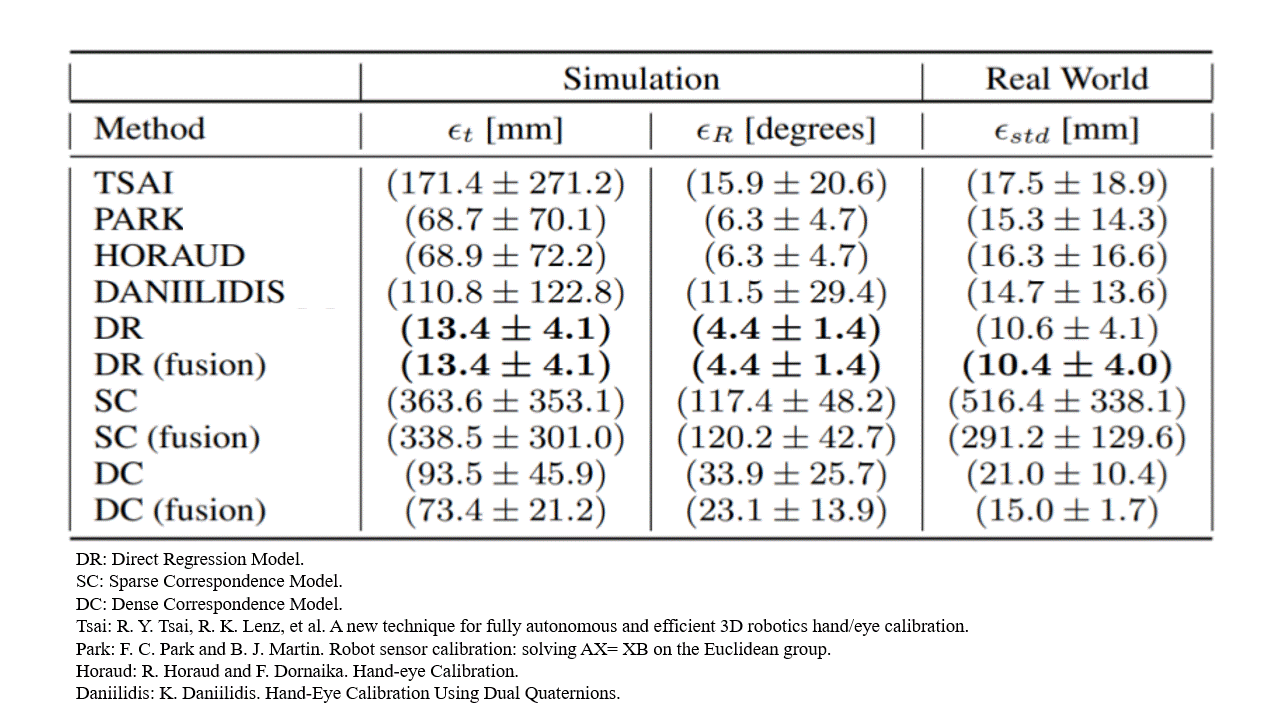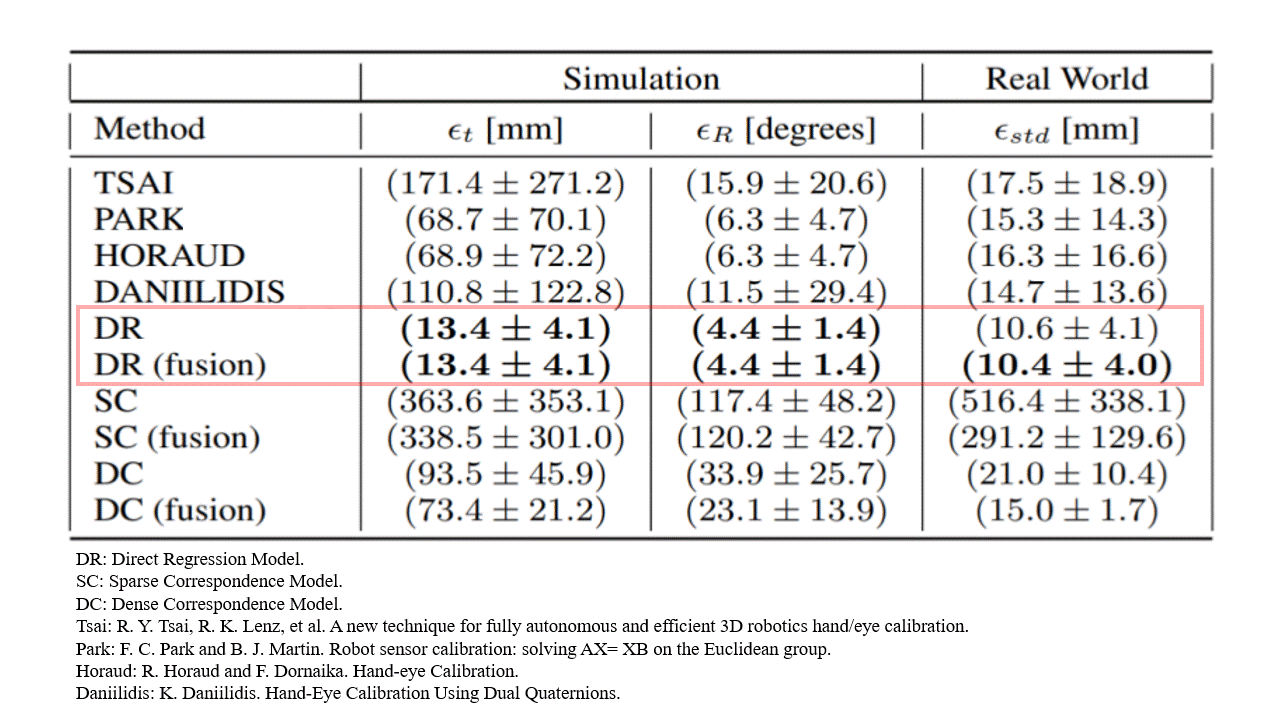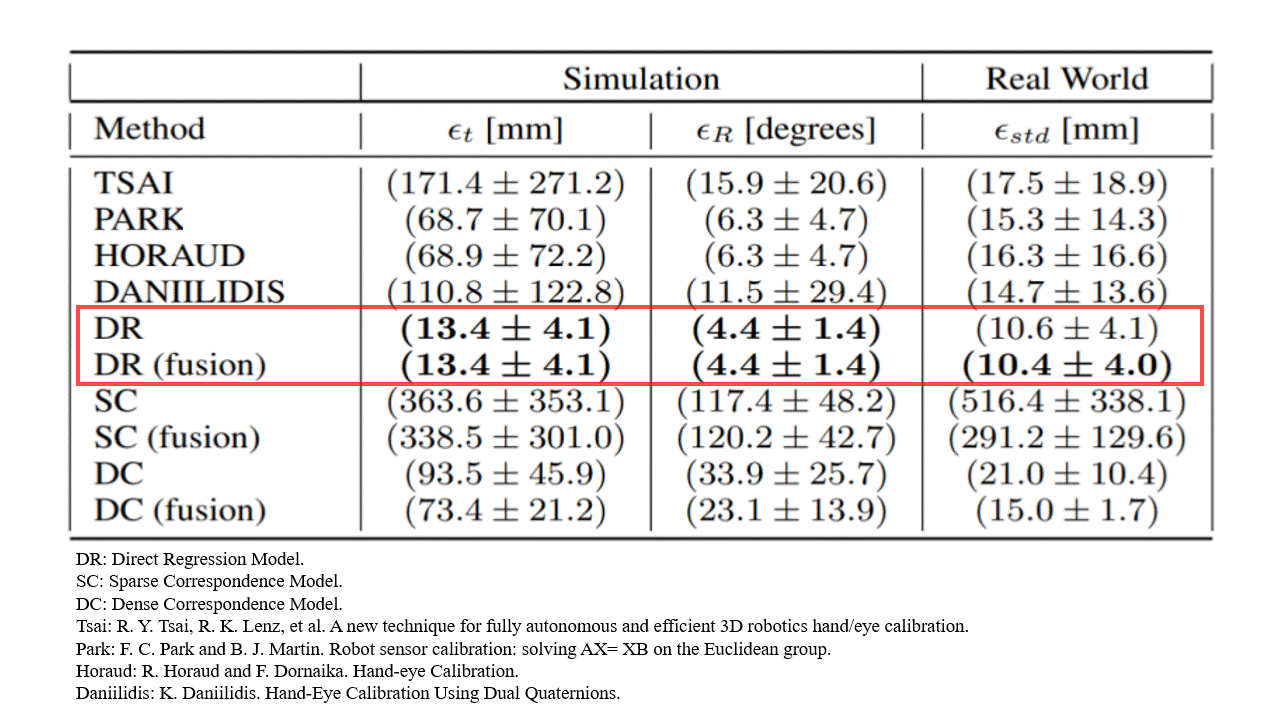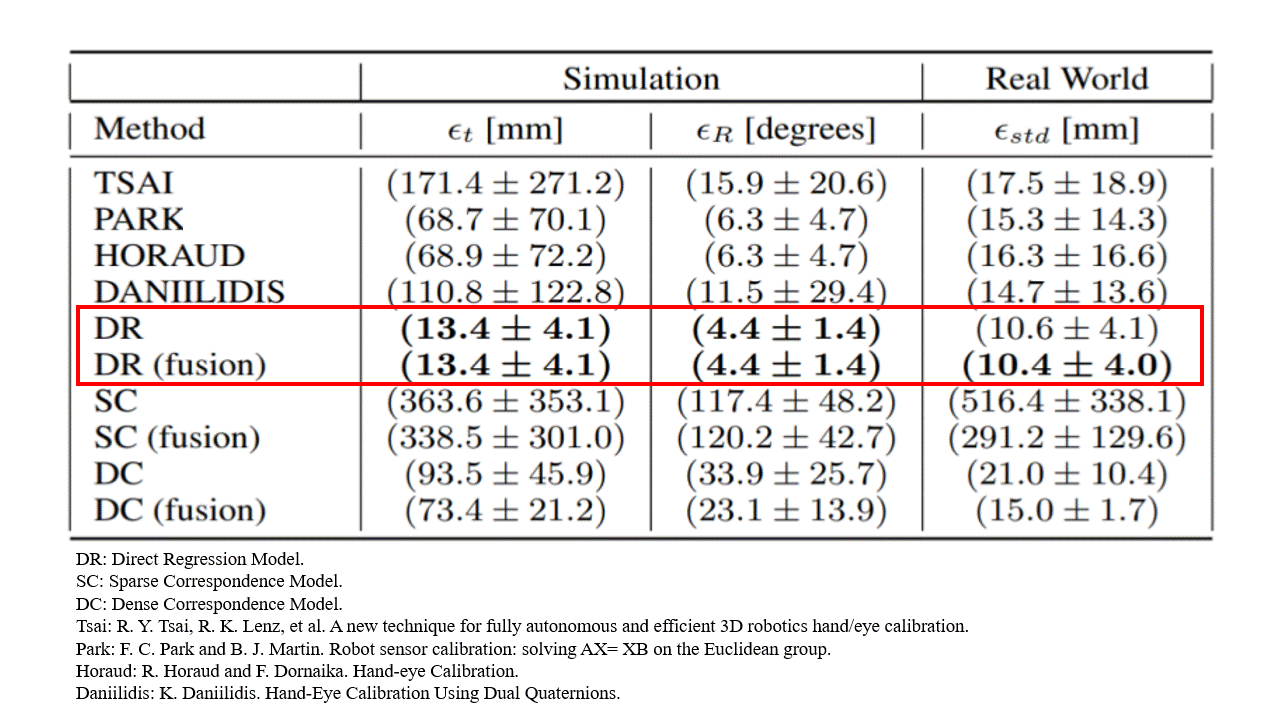
Results & Analysis

Surprisingly, we find that the direct regression model outperformed both the classical baselines and the geometry-based deep learning alternatives.

Analysing this result, we find several interesting properties that become apparent.

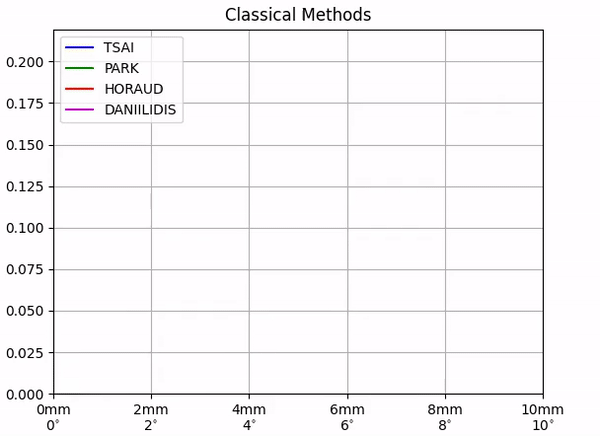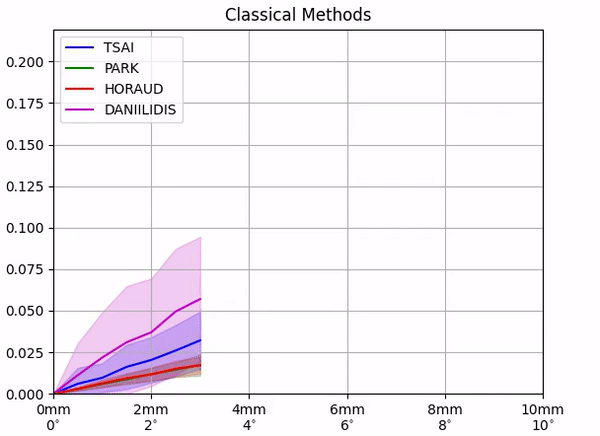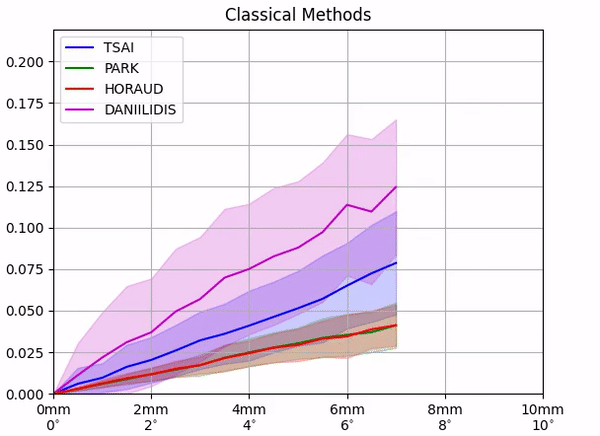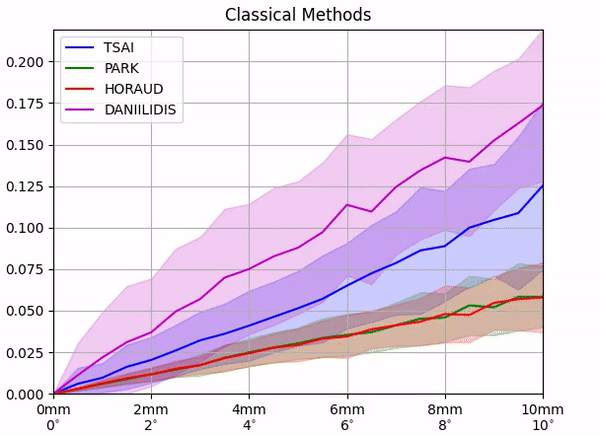
Calibration position error [m]

First, for the classical methods, we perform a controlled noise experiment in simulation. Fixing all other variables to their ground truth values, we inject increasing amounts of the noise in the pose of the calibration object and compute the corresponding errors in the calibration.

We find that although with perfect information the classical methods output exact calibrations, their performance quickly deteriorates with increasing the amount of noise in the system.

Noise in the tag position

Calibration position error [m]

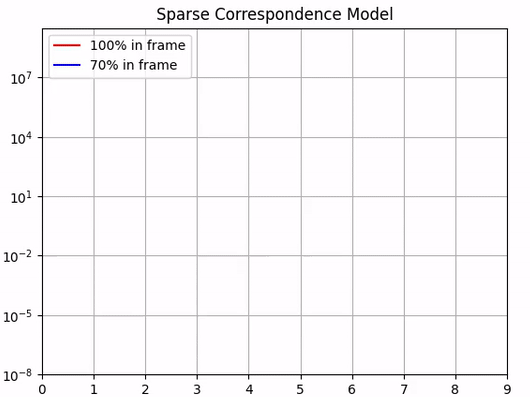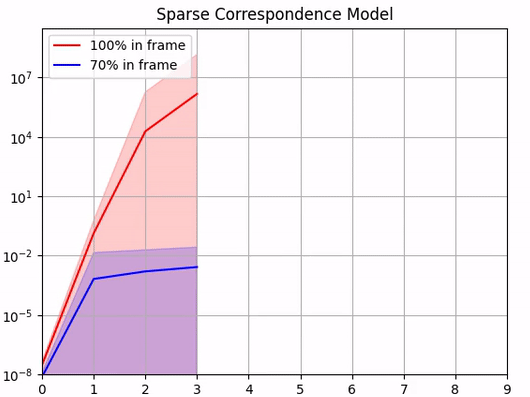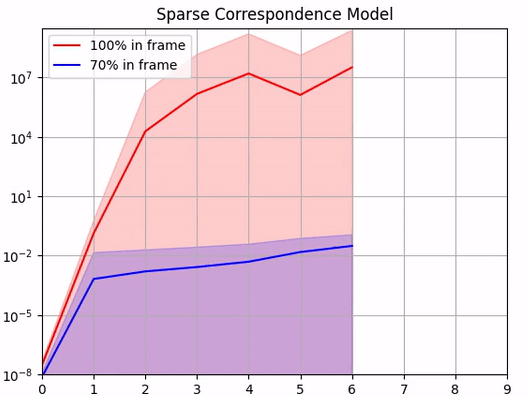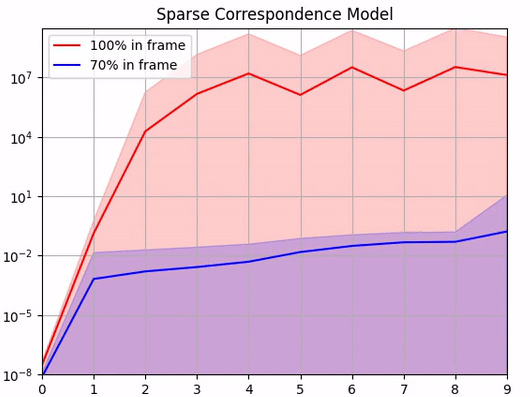
For the sparse correspondence model, we adopt a similar approach: We study the effect of noise in predicted 2D keypoint locations on PnP pose estimation. We consider two sets of keypoints. The first is clustered on the tip of the gripper fingers and appeared in 100% of the training images, and the second is more spaced out and appeared in 70% of the training images.

We again find that, although able to recover the ground truth extrinsic matrix when there is no noise in the predicted keypoints locations, the calibration quality quickly deteriorates as soon as we introduce errors. Since this deterioration is very fast, there is not much tolerance in the system for errors in the neural network predictions.

Noise in the keypoint location [pixels]

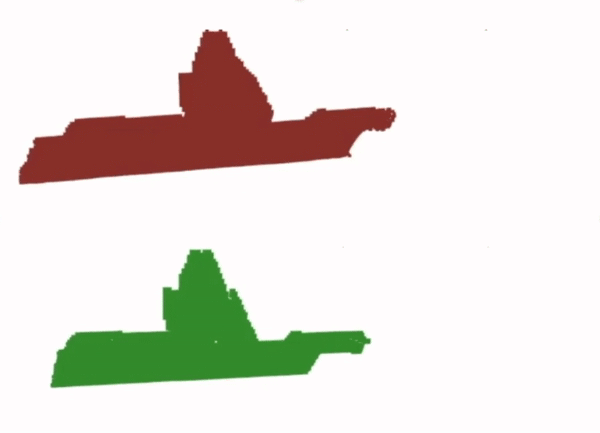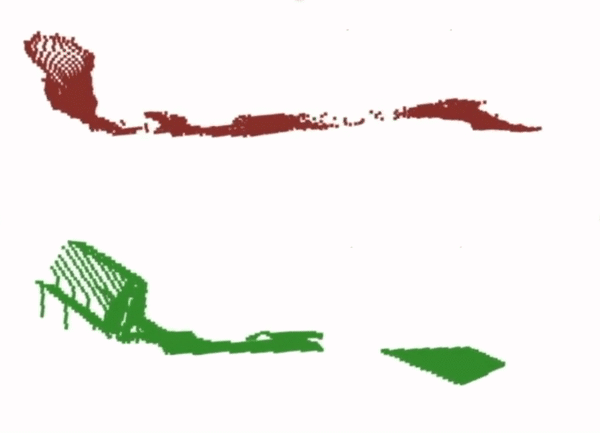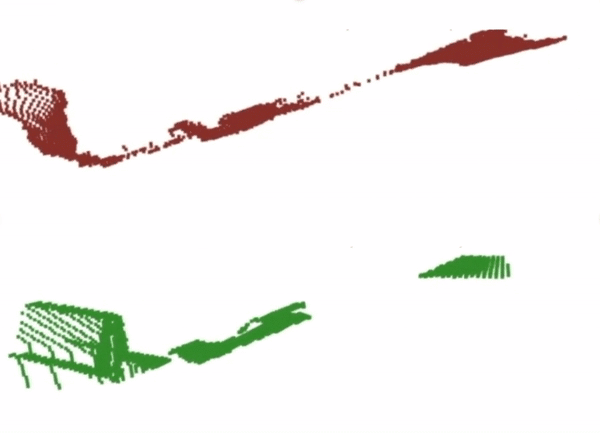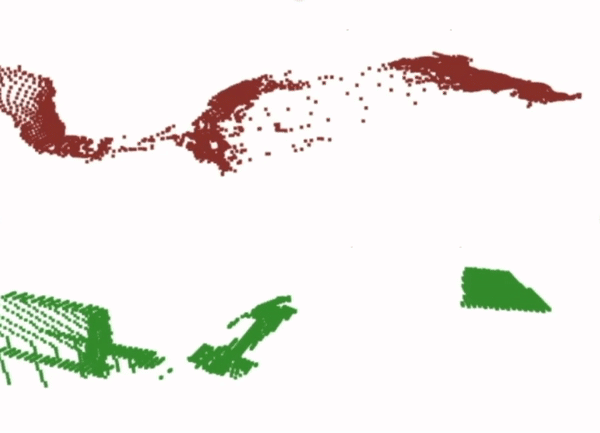
Finally, for the dense correspondence model, we analyse the outputs of depth prediction network. We find that the performance seems to suffer from the smoothness bias of neural networks, which makes them struggle to reproduce the discontinuous jumps in depth required in order to produce an accurate point cloud for the end-effector.

Prediction

Ground Truth